Zero Knowledge (ZK)

Autor - Gelois & Israel - Jun '25

Introducción

Las pruebas de conocimiento cero (Zero-Knowledge Proofs o ZKP) representan uno de los avances más fascinantes en la criptografía moderna. Este método criptográfico permite a una persona (el probador) demostrar a otra (el verificador) que posee cierta información sin revelar absolutamente nada sobre dicha información, excepto el hecho de que la posee.

Concebidas originalmente en 1985 por Shafi Goldwasser, Silvio Micali y Charles Rackoff en su influyente publicación "The Knowledge Complexity of Interactive Proof-Systems", las ZKP establecen un sistema de prueba compuesto por tres elementos fundamentales: el probador, el verificador y un desafío. En esencia, resuelven una aparente paradoja: ¿cómo demostrar que conoces un secreto sin revelar el secreto mismo?

Cómo funcionan las pruebas zk?

Los Tres Pilares Fundamentales

Todo protocolo ZKP debe satisfacer tres criterios esenciales:

1. Completitud: Si dices la verdad y sigues las reglas, siempre convencerás al verificador. No hay falsos negativos en este juego.

2. Solidez: Es prácticamente imposible engañar al sistema. Un mentiroso será descubierto casi con total seguridad, convirtiendo la trampa en una apuesta perdida.

3. Conocimiento cero: El verificador termina el proceso exactamente como empezó: sin conocer nada nuevo excepto que el probador no miente.

Los Protagonistas del Protocolo

Como en toda buena historia, tenemos personajes con roles bien definidos:

• El Probador: Posee el secreto y busca demostrarlo sin revelarlo.

• El Verificador: Cuestiona y examina para confirmar la verdad sin aprender el secreto.

• La Declaración: La afirmación que se intenta probar, desde conocer una contraseña hasta poseer una clave criptográfica.

• Elemento básicos

  En su forma más básica, tres movimientos elegantes:

  • El Testigo: El secreto que el probador conoce. Este conocimiento le permite responder preguntas que solo alguien con esta información podría contestar correctamente.

  • El Desafío: El verificador selecciona preguntas aleatorias que ponen a prueba el conocimiento del probador.

  • La Respuesta: El probador contesta calculando la solución sin revelar el secreto subyacente. Cada respuesta correcta aumenta la confianza del verificador.

La repetición de estos pasos reduce drásticamente la posibilidad de que alguien sin el conocimiento real pueda engañar al sistema por simple suerte. añadimos

Comprendiendo fundamentos matemáticos de zk

NARK

Un NARK (Argumento no interactivo de conocimiento) es un tipo de prueba criptográfica en la que el probador demuestra a un verificador que conoce un testigo (un valor privado) que satisface una cierta afirmación (un circuito o una función computacional), sin revelar nada sobre ese testigo.

Modelo Computacional: Preprocesamiento

Circuito Aritmético (computación): Dado un circuito C, toma entradas públicas x y entradas privadas w, y produce un valor en el campo F:

$$C(x,w)→F$$

• x: entrada pública (pública para el verificador).

• w: entrada privada, también conocida como testigo o witness (privada para el probador).

Algoritmos

Algoritmo de Preprocesamiento

S: Dado un circuito C, el algoritmo de preprocesamiento genera parámetros públicos pp y parámetros privados vp.

$$S(C)→(pp,vp)$$

• pp: parámetros públicos, que estarán disponibles para el probador.

• vp: parámetros privados, que estarán disponibles para el verificador.

Algoritmo del Probador

P: El probador genera la prueba, utilizando los parámetros públicos pp, las entradas públicas x y el testigo privado w.

$$P(pp,x,w)→proof$$

• La prueba es un conjunto de datos que demuestra que el probador sabe el testigo w tal que C(x,w)=0.

Algoritmo del Verificador

V: El verificador toma los parámetros privados vp, las entradas públicas x y la prueba generada por el probador, y verifica si la prueba es válida.

$$V(vp,x,proof)→aceptar/rechazar$$

• Si la prueba es válida, el verificador acepta. Si no, la rechaza.

Propiedades de un NARK:

✅ Completeness

Si el probador conoce un testigo válido, el verificador siempre acepta:

$$Pr[V(vp,x,P(pp,x,w))=accept]≈1$$

✅ Knowledge Soundness

Si una prueba es aceptada, se garantiza que el probador conoce un testigo w tal que C(x,w)=0.

✅ Zero-Knowledge (opcional)

La prueba no revela ninguna información sobre el testigo w. Existen simuladores eficientes capaces de generar pruebas indistinguibles de las reales sin conocer w.

Snark

SNARK = S and NARK

• Succinct

  • Tamaño de prueba: sublineal respecto al tamaño del testigo w

  • Tiempo de prueba: sublineal respecto al tamaño del circuito C

• Strongly Succinct

  • Tamaño de prueba: logarítmico en el tamaño del circuito C

  • Tiempo de prueba: logarítmico en el tamaño del circuito C

• Circuito

  • El verificador no tiene tiempo de leer el circuito

Conceptos Clave y Operaciones

zk-SNARKs

Los zk-SNARKs (SNARKs de conocimiento cero) permiten probar que conocemos variables testigos

w que satisfacen F(x,w)=y para una función F y una instancia pública x, sin revelar información sobre w.

¿Cómo se relaciona un zk-SNARK con un NARK?

• Un SNARK es un NARK que además es sucinto

• Un zk-SNARK es un SNARK que además es zero-knowledge

zk-SNARK=Succinct+Non-interactive+Argument of Knowledge+Zero-Knowledge

$$zk-SNARK=Succinct+Non-interactive+Argument of Knowledge+Zero-Knowledge$$

• Respecto al nombre:

• Succinct: las pruebas deben ser breves y rápidas de verificar. Esto permite delegar cálculos costosos a partes no confiables y verificar su validez sin ejecutar el programa uno mismo.

• Non-interactive: no requiere interacción entre probador y verificador, ni para generar ni para verificar la prueba. Se logra mediante la transformación de Fiat-Shamir.

• Argument of Knowledge: podemos probar con alta probabilidad que conocemos el testigo.

Tipos principales:

• Marlin (Aleo)

• PLONK

• STARKs

• Groth16

• Bulletproof

Comparación Rápida de Algoritmos ZKP

Algoritmo	Prueba	Verificación	Setup	Post-Cuántico
Groth'16	Excelente ~200B	Excelente ~1.5ms	Regular (Por circuito)	No
PLONK/Marlin	Bueno ~400B	Bueno ~3ms	Bueno (Universal)	No
Bulletproofs	Regular ~1.5KB	Débil ~3s	Excelente (Transparente)	No
STARK	Débil ~100KB	Regular ~10ms	Excelente (Transparente)	Sí

Resumen Visual

• Mejor tamaño: Groth'16 < PLONK < Bulletproofs < STARK

• Más rápido: Groth'16 < PLONK < STARK << Bulletproofs

• Más confiable: STARK = Bulletproofs > PLONK > Groth'16

• Futuro seguro: STARK > Todos los demás

Elementos para contruir a Snark

Esquemas de Compromiso de Polinomios y Argumentos de Conocimiento

• Esquema de Compromiso de Polinomios

  • Permite obtener un argumento interactivo sucinto:

    • Se compromete (commit) un polinomio.

    • Se vincula (bind) el compromiso al polinomio original.

    • Luego se pueden evaluar los valores del polinomio sin revelarlo completamente.

• Prueba de Oráculo Interactiva (IOP - Interactive Oracle Proof)

  • Se utiliza para verificar la satisfacibilidad de circuitos o sistemas R1CS.

  • Permite evaluar polinomios comprometidos en uno o múltiples puntos, a lo largo de varias rondas.

  • Extiende los compromisos de polinomios al modelo general de satisfacibilidad.

• Heurística de Fiat-Shamir

  • Transforma una prueba interactiva en una prueba no interactiva.

  • Sustituye los desafíos aleatorios del verificador por un hash determinista de la transcripción hasta ese punto.

Construcción de SNARKs

Beneficios y Aplicaciones de las Pruebas zk

Las pruebas de conocimiento cero están redefiniendo el equilibrio entre verificación y privacidad, ofreciendo ventajas significativas en aplicación:

• Pagos anónimos

  • Ocultan montos, remitentes y destinatarios en transacciones.

  • Protegen la privacidad financiera frente a proveedores, bancos y autoridades.

  • Habilitan “privacy coins” (Zcash) y servicios como Tornado Cash para transferencias completamente privadas.

• Protección de identidad

  • Verifican atributos personales (ciudadanía, mayoría de edad) sin exponer datos sensibles.

  • Facilitan la identidad descentralizada (“self-sovereign”) donde cada usuario controla qué se revela.

  • Eliminan la necesidad de compartir pasaportes, números fiscales o documentos completos.

    
• Autenticación simplificada

  • Permiten acceder a plataformas sin transmitir contraseñas ni almacenar grandes volúmenes de datos.

  • Generan pruebas basadas en entradas públicas (pertenencia a un servicio) y privadas (credenciales del usuario).

  • Mejoran la experiencia de usuario y reducen el riesgo de brechas de seguridad.

  
• Computación verificable (off-chain scaling)

  • Externalizan la ejecución de cálculos a cadenas o servicios externos, reduciendo la carga en la red principal.

  • Usan pruebas de validez para aplicar resultados sin re-ejecución, mejorando throughput y velocidad.

  • Base de soluciones como ZK-rollups y validiums en Ethereum.

    
• Votación resistente a sobornos y colusión

  • Garantizan votos anónimos, auditables y a prueba de censura.

  • Impiden la identificación de preferencias individuales y la coordinación de sobornos.

  • Mantienen la integridad electoral sin sacrificar privacidad.

    

Aplicaciones ZKP

Categoría	Beneficio Principal	Lo Más Destacado	Por Qué
Blockchain – Identidad	Verifica identidad sin exponer datos personales	Autenticación sin contraseñas	Protege la privacidad en accesos digitales
Blockchain – Cadena de Suministro	Valida orígenes y trazabilidad sin revelar secretos internos	Transparencia controlada	Cumple normativas y refuerza la confianza
Blockchain – Interoperabilidad	Facilita puentes seguros entre cadenas	Transferencias cross-chain privadas	Conecta ecosistemas sin exponer datos sensibles
Blockchain – Almacenamiento	Comprueba integridad de datos y cálculos off-chain	Almacenamiento cifrado verificable	Ideal para datos sensibles en redes descentralizadas
Blockchain – Privacidad nativa (L1)	Incorpora protección de datos desde el diseño de la cadena	Privacidad integrada	Seguridad garantizada sin capas adicionales
Blockchain – Escalado (L2)	Aumenta throughput y reduce costos	Rollups ZK y validiums	Descarga transacciones off-chain manteniendo validez
Blockchain – Transacciones confidenciales	Oculta montos y participantes	Confidential Transactions & Bulletproofs	Protege la información financiera en on-chain
Blockchain – Prueba de Reservas	Demuestra solvencia de exchanges sin revelar balances privados	Confianza pública	Evita fraudes y auditorías invasivas
No-Blockchain – Verificación de atributos	Comprueba propiedades (edad, solvencia…) sin exponer datos completos	Credenciales anónimas	Reduce la exposición de información personal
No-Blockchain – Sistemas multiusuario	Potencial privacidad y control granular en entornos compartidos	Interacciones seguras (MUI)	Protege datos de múltiples usuarios simultáneamente
No-Blockchain – Votación electrónica	Garantiza privacidad y auditabilidad de votos	Votos anónimos verificables	Refuerza la integridad electoral sin revelar preferencias
No-Blockchain – ML confidencial	Verifica inferencias y entrenamientos sin compartir datos	Modelos confiables	Crucial para sectores regulados (salud, finanzas)

Para saber mas en aplicaciones:

• A Survey on the Applications of Zero-Knowledge Proofs

Desafíos y Limitaciones de las Pruebas zk

• Complejidad de Implementación

  • Requieren conocimientos criptográficos avanzados, lo que dificulta su adopción por organizaciones sin experiencia especializada.

• Costos de Hardware

  • Generar pruebas implica cálculos intensivos que exigen hardware especializado y costoso.

• Costos de Verificación

  • La verificación también es exigente, aumentando los costos, especialmente en blockchains donde impacta en tarifas de gas.

• Configuración Confiable (en ZK-SNARKs)

  • ZK-SNARKs dependen de una ceremonia inicial segura. Si se compromete, afecta la confianza y la seguridad.

  • ZK-STARKs evitan este problema usando aleatoriedad pública.

• Sobrecarga de Rendimiento

  • Las ZKPs pueden ralentizar los sistemas debido a su alta demanda computacional.

• Amenaza Cuántica

  • ZK-SNARKs basados en curvas elípticas son vulnerables a computadoras cuánticas.

  • ZK-STARKs ofrecen mayor resistencia.

Recapitulación de ZKP

Las Pruebas de Conocimiento Cero (ZKP) demuestran posesión de información sin revelarla.

Funcionamiento: Interacción de desafío y respuesta para verificar el conocimiento del Testigo.

Fundamentos:

• NARK: Prueba no interactiva de conocimiento.

• SNARK: NARK sucinto (rápido y pequeño).

• zk-SNARK: SNARK con privacidad (cero conocimiento).

• Tipos: Groth'16, PLONK/Marlin, Bulletproofs, STARKs.

Construcción (SNARKs):

• Compromiso Polinomial.

• Prueba de Oráculo Interactiva (IOP).

• Heurística de Fiat-Shamir (para no interactividad).

Beneficios:

• Privacidad en transacciones e identidad.

• Autenticación eficiente.

• Escalado de computación.

• Votación segura.

• Aplicaciones en blockchain y fuera de ella.

Desafíos:

• Implementación compleja.

• Costos computacionales (prueba y verificación).

• Setup confiable (en algunos zk-SNARKs).

• Rendimiento.

• Resistencia cuántica (limitada en algunos tipos).

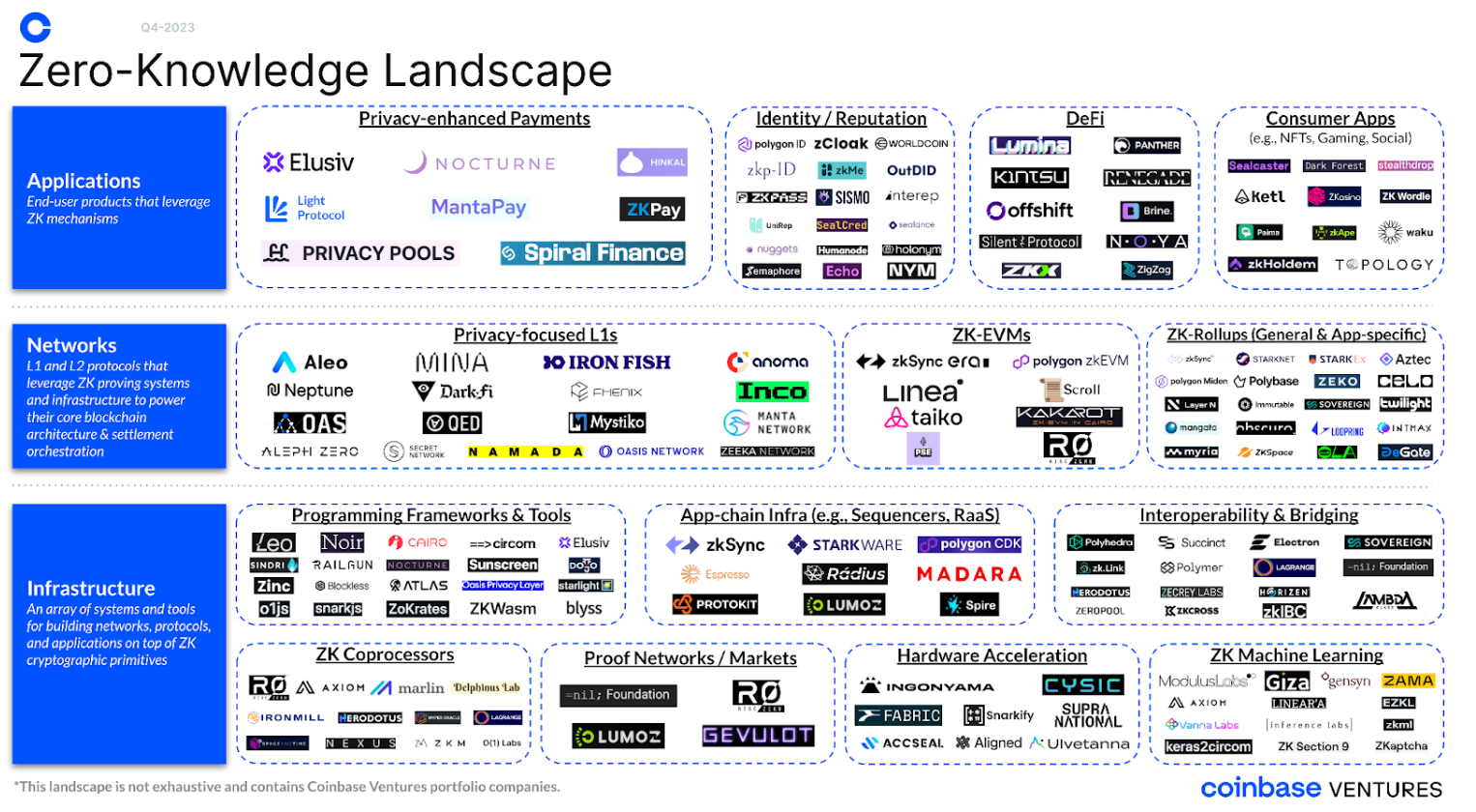
ZK Landscape de los proyectos